How to Make Smarter Decisions with Bayesian Thinking

In 1763, a revolutionary paper on human thinking was published in the Philosophical Transactions of the Royal Society. The author, Thomas Bayes, had died two years earlier, never knowing his work would fundamentally change how we reason about uncertainty. The paper, edited and submitted by his friend Richard Price, contained what we now know as Bayes' Theorem.
We're drowning in information today, but our struggle to make sense of uncertainty isn't new. In Bayes' time, the Age of Enlightenment was flooding Europe with new discoveries, theories, and contradictions. Scientists and philosophers grappled with fundamental questions: How do we learn from experience? How can we update our beliefs when new evidence challenges old certainties? How do we reason when we don't have all the pieces?
Bayes offered an elegant solution. Instead of demanding absolute certainty—an impossible standard in our messy reality—he provided a mathematical framework for learning from experience. His theorem showed how to systematically update our beliefs as new evidence emerges, transforming probability from a static measurement into a dynamic tool for understanding.
The implications were revolutionary, even if few recognized it at the time. It would take another century before Bayes' ideas would begin to transform fields from science to warfare, from medicine to artificial intelligence. During World War II, Alan Turing used Bayesian methods to crack the German Enigma code. Today, spam filters use Bayes' Theorem to identify unwanted emails, doctors use it to interpret test results, and scientists use it to update their understanding of the universe.
But Bayes' true gift wasn't just mathematical—it was philosophical. When algorithms feed us an endless stream of information, when social media amplifies certainty while burying nuance, when we’re degenerating into a shit-slinging species of polarized, angry keyboard warriors, Bayesian thinking offers a different path. It teaches us that knowledge isn't about achieving perfect certainty, but about systematically reducing uncertainty. It reminds us that our beliefs should be fluid, not fixed—ready to adapt when new evidence emerges.
The world has changed dramatically since Thomas Bayes pondered probability in his English garden. But his central insight is more relevant than ever: in a world of uncertainty, the best we can do is reason systematically about what we know, remain humble about what we don't, and update our understanding as new evidence emerges. It's a guide for thinking clearly in a fucked up and complex world.
What Does Bayes’ Theorem Really Say?
TL:DR - Bayes’ Theorem tells you how to update your understanding when faced with new evidence. Here’s the formula:
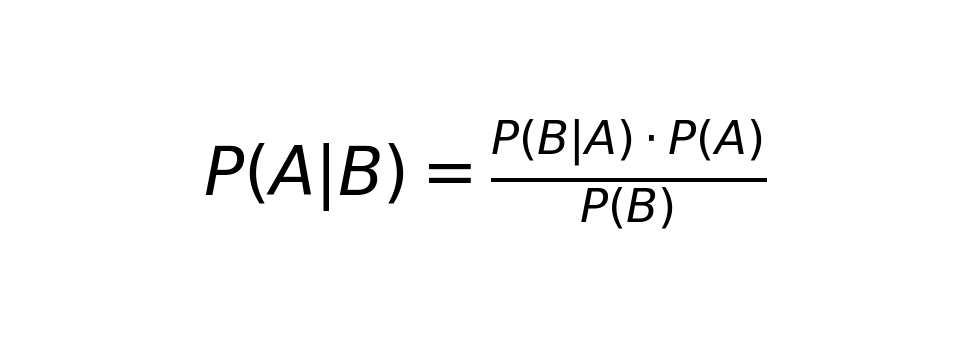
It might look intimidating, but its logic is simple. Break it down, and you get:
- Posterior probability : How likely your hypothesis is after considering the evidence.
- Likelihood : How probable the evidence is if your hypothesis were true.
- Prior probability : Your initial assumption or belief about the hypothesis.
- Marginal likelihood : The total probability of the evidence across all possibilities.
In plain terms, Bayes’ Theorem helps you answer:
What should I believe now, given what I believed before and what I’ve just learned?
It’s a mathematical way of doing what we try to do intuitively—just without the guesswork and cognitive bias.
The Power of Bayes
Example: Imagine you're an investor trying to predict whether a stock will rise or fall. Your starting point - what Bayesians call your "prior probability" - comes from your initial research. Let's say based on historical performance, industry trends, and market conditions, you estimate a 60% chance the stock will rise. This isn't just a guess - it's your informed starting belief.
Then new evidence arrives: a surprisingly strong quarterly report. This is where Bayes’ Theorem becomes powerful. Instead of simply jumping to a new prediction, you systematically update your original 60% estimate by considering how likely you would have been to see such strong earnings if your "stock will rise" hypothesis was correct, versus if it was wrong.
Let's put some numbers to this:
- Prior probability (initial belief): 60% chance of stock rising
- Likelihood of strong earnings given stock is healthy: 80%
- Likelihood of strong earnings given stock is weak: 20%
Using Bayes' Theorem, you can calculate your new, updated probability. The strong earnings report would shift your confidence from 60% to roughly 86% - a much stronger conviction, but still acknowledging uncertainty.
This Bayesian approach has 4 key advantages:
- It forces discipline - you must explicitly state your initial beliefs
- It helps avoid overreaction - you update beliefs gradually, not drastically
- It keeps you humble - every prediction maintains a degree of uncertainty
- It creates a learning system - each new piece of evidence refines your model
Most importantly, Bayesian thinking acknowledges that market predictions are never about certainty, but about constantly refining probabilities as new information arrives. This matches the reality of markets far better than approaches that claim to offer absolute certainty.
When an investor thinks like a Bayesian, they're less likely to panic sell on bad news or become overconfident on good news. Instead, they systematically update their views, maintaining a balance between learning from new evidence and not overreacting to market noise.
Example 2: You can think of your email inbox as a busy customs checkpoint, with your spam filter playing the role of a particularly clever guard who uses Bayesian reasoning to spot suspicious packages (emails).
Your spam filter starts with some basic knowledge—what statisticians call "prior probabilities." It knows, for instance, that about 45% of all email traffic is spam. But rather than stopping there, it uses Bayes' Theorem to get smarter with every email it processes.
When a new email arrives, the filter examines its characteristics: Does it contain phrases like "FREE MONEY" or "Dear Sir/Madam"? Was it sent at 3 AM? Is it from a new domain? For each of these features, the filter knows two crucial probabilities: how often they appear in spam versus legitimate emails.
Bayes' Theorem combines all these clues with that initial 45% baseline to calculate the probability that this particular email is spam.
Let's say an email arrives with the phrase "wire transfer."
The filter knows:
- 90% of emails containing "wire transfer" that turned out to be spam
- 10% of legitimate emails contain this phrase
- Combined with other factors like sender reputation and timing
Using Bayes' Theorem, the filter continuously updates its beliefs. If a trusted colleague regularly sends emails about wire transfers, the filter learns to adjust its calculations for that specific sender. If users frequently mark certain types of messages as "Not Spam," the filter recalibrates its probabilities.
This is why modern spam filters are so effective—they're not just following static rules, they're constantly learning and updating their understanding of what constitutes spam, just as a customs officer becomes better at spotting suspicious packages through experience. The beauty of Bayesian filtering is that it mimics how humans naturally refine their judgment: starting with general assumptions, then updating them based on new evidence.
How to Think Like a Bayesian
Want to apply this to your own decisions? Here’s a step-by-step guide:
- Define the question. What are you trying to decide?
- Example: Should I bring an umbrella tomorrow?
- Set your starting belief. Use what you know so far.
- Example: In fall, it rains 50% of the time.
- Add new evidence. Look for reliable data.
- Example: The weather forecast says 70% chance of rain.
- Update your belief. Combine the old and new information.
- Example: Now, you’re 85% sure it will rain, so you grab the umbrella.
Bayesian Thinking Simplified: A 3-Step Process
- Start with your baseline belief (Prior).
Ask: “Before I learned this new information, what did I already believe about this situation?”
- Weigh the new evidence (Likelihood).
Ask: “If my belief is true, how likely is it that I would see this new evidence? And if my belief is false, how likely is it?” Focus on the strength of the evidence—strong signals move your belief more, weak signals less.
- Adjust your belief (Update).
Ask: “Does this new evidence make me more or less confident? By how much?" Combine your baseline belief with the weight of the evidence to refine your confidence.
The Easy-to-Remember Formula
New Belief = Old Belief + (Strength of Evidence × Confidence Adjustment)
- If the evidence strongly supports your belief, increase your confidence.
- If the evidence goes against your belief, decrease your confidence.
- If the evidence is weak or uncertain, make only a small adjustment.
Why Bayesian Thinking Works
- It Combines Knowledge and Evidence Seamlessly
- Bayesian reasoning lets you start with what you know (or think you know) and adjust as new data comes in. Whether you’re a doctor relying on years of experience or an investor analyzing market trends, this ability to merge prior knowledge with current evidence is invaluable.
- It’s a Fit for a Changing World
- Life doesn’t hand you all the evidence at once. As new information arrives, Bayesian methods allow you to update your beliefs dynamically. This flexibility is crucial in fast-moving environments like medicine, finance, or even political decision-making.
- It Embraces Uncertainty Without Fear
- Uncertainty is often seen as a flaw, but Bayesian thinking turns it into a strength. By forcing you to quantify probabilities, it keeps you honest—no wild guesses, no unjustified confidence. Just clear, rational decision-making.
Why Bayesian Thinking is Hard
Imagine you’re solving a mystery. Bayesian thinking is like being a detective—it helps you update your beliefs as you uncover new clues. It’s powerful, but it’s not always easy.
Problem 1: Starting With the Right Assumptions
In Bayesian thinking, you begin with a “prior,” which is just a fancy way of saying your starting belief about how likely something is. For example, if someone tells you it’s going to rain tomorrow, you might think, “It rained yesterday, so maybe there’s a 50% chance.” That’s your prior.
The tricky part? If your prior is wrong, everything you build on it will be wrong, too. It’s like guessing a puzzle piece will fit because it looks close—only to find out it’s from a different puzzle. The good news is, if you have solid data to work with, you can adjust your prior and get back on track.
Problem 2: The Math Can Be a Headache
Once you’ve got your prior, you need to update it when new evidence comes in. That’s where Bayes’ Theorem comes in—a formula that tells you how to adjust your belief based on the strength of the new clue.
Think of it like baking cookies. If the recipe says “bake for 10 minutes” but your cookies look raw after 10 minutes, you’d update your plan and bake them longer. Bayesian math is like that adjustment—except it uses numbers to tell you how much longer to bake.
The problem? When you’re dealing with a lot of clues (or data), the math can get really messy. Imagine trying to bake cookies with 20 different recipes all mixed together.
Start with a rough guess (e.g., “I think there’s a 40% chance this is true”) and then adjust it based on how strong the new evidence feels to you. For personal decisions, look at your past experiences. If you don’t have data, think about patterns. For example, if you know someone is late 3 out of 5 times, start with a 60% chance they’ll be late again. It won’t be perfect but can still guide your decisions.
Problem 3: Garbage In, Garbage Out
The last big challenge is the data itself. Bayes’ Theorem only works if the evidence you’re using is accurate. If the clue you’re working with is wrong—like a witness in your mystery who gives a bad description—you’ll end up with the wrong conclusion.
Worse, sometimes people forget to include key parts of the formula, like the “marginal likelihood.” That’s a fancy term for asking, “How likely is this evidence, no matter what’s true?” Ignoring it is like skipping a step in a recipe—you might still get cookies, but they’ll taste like shit.
Why It’s Still Worth It
Bayesian thinking is more than a mathematical tool—it’s a way of approaching the world with humility, curiosity, and rigor. It challenges us to acknowledge what we truly know, admit what we don’t, and embrace the constant flux of new information. We thrive too much on overconfidence and snap judgments lately. And it makes Bayesian thinking a quiet act of rebellion. Think deliberately, update our beliefs without pride or shame, and let evidence—not intuition or ideology—be our guide.
This mindset is for anyone navigating the messy uncertainties of life. Bayes forces us to confront the reality that truth isn’t handed to us—it’s something we have to earn, by making peace with uncertainty, understanding that it’s not a failure of knowledge but a fundamental part of how the world works.
Take a look at the world right now.
Are we happy with how it looks?
We're angry. Misinformed, but convinced we're right. We're sitting on top of a powder keg.
We have to learn to think smarter, adapt faster, and approach problems with a detective’s precision: weighing every clue, discarding bad leads, and refining our understanding step by step. The world may be unpredictable, but Bayesian thinking offers a framework to make sense of it—one update at a time.





